
机器人的定位,运动等,和数学显然是无法分开的。如果把研究机器人比作做菜的话,数值分析就是颠锅一样的基本功,没有它能做菜,但做不好菜😶🌫️
关于这篇博客去年就想开始写了,拖到了现在才开动,不知道上课学的知识还记得多少,就当是复习一下吧😃😃😃
数值分析这门课并没有选上(选的人实在是太多了),不过最后还是一节不落的听完了(除了最后的习题课)。这门课非常有趣且实用,特别是赵熙乐老师上课一边讲解数学原理,一边现场编程演示,利用计算机解决各种数学问题,让我感受到了数学的和编程的之间可以如此和谐。
这个系列不知道要写多久,有空的时候就更新一下吧😊。
不积跬步,无以至千里;不积小流,无以成江海
误差
误差通常是指某一元素的观测值和真值之间的差值,误差有时候很讨厌(不想要误差)有时候却很有用(用于优化得到预测),数值分析从这里开始最好不过了。
误差的衡量
一般情况下,我们把误差分为绝对误差和相对误差,绝对误差的定义如下,很好理解,就代表了一个计算的数值和其真值之间的差距: \[ e(x) = x-x^* \]
有时候绝对误差并不能很好的衡量误差的影响,比如0.1的误差对于真值999999和0.2两个数的影响是完全不一样的。而相对误差的作用就体现出来了: \[ e_r(x)=\frac{e(x)}{|x^*|} \] 有时也写作: \[ e_r(x)=\frac{e(x)}{|x|} \]
误差的分类
模型误差:有些问题要用数学方式表达很困难,通常选择一个近似的数学模型,所带的误差为模型误差。
观测误差:物理量的观测通常有误差,很好理解。
截断误差:
通常情况,对于一个复杂的函数,要计算其值,通常是采用近似的方法,比如计算\(\ln(2)\),我们知道\(\ln(x+1)\)的泰勒展开如下: \[ ln(x+1)=x-\frac{1}{2}x^2+\frac{1}{3}x^3-\frac{1}{4}x^4+\cdots+(-1)^{n-1}\frac{1}{n}x^n+\cdots \]
计算\(ln(2)\)我们只需把\(x=1\)带入上述表达式中,但是由于其泰勒展开无限长,我们显然没法计算其精确解,一般我们会取前面几项。这样由于截断产生的误差就为截断误差。
舍入误差:舍入误差就是指计算机无法精确的表示一个小数引起的误差。
误差有时候会以意想不到的方式捣乱,而有时候一个算法表现不如意却有可能是误差引起的。下面通过讲解计算机中浮点数的误差直观的理解计算机数学和纯数学之间的区别。同时为了更清楚的了解舍入误差,我先介绍一下计算机中小数是如何表示的。
浮点数
计算机做数学运算和现实中的数学运算有点不一样,计算机无法表示连续的量,计算机一般用浮点数表示连续的量,浮点数可以简单的定义如下:

我们想要将一个数\(f\)转化为浮点数,首先分别将整数部分和小数部分用二进制表示,再通过右移保证最高位为1(\(f\)小于1的时候特殊处理),将尾数M和右移的尾数E保存起来,就得到了浮点数,如下所示: \[ f=S1.M\times2^E=S1.ME\ll E \] 32位浮点数的标准如下所示:

通常情况下,计算机浮点数的舍入误差为\(1e-16\)
误差的传播
举一个简单的误差传播例子,有个方程的迭代形式如下所示: \[ y_n=1-ny_{n-1} \] 那么它误差的累积和n之间的关系有:\(eps_n=n!\cdot eps_0\),我们不断迭代计算上述方程,迭代10次时,误差约为\(3.6\times 10^6eps_0\),误差被放大了100000倍!而迭代20次后,误差为\(2.4\times 10^{19}eps_0\)!!!
迭代思想
计算机数学还有一个特点,那就是对于简单的数学运算处理特别快,这带来的好处就是我们可以用一些迭代的算法,通过计算机强大的计算能力不断迭代,从而解决一个复杂的问题。比如我们通过迭代法计算表达式\(f(x)=0\)的解,假设解为\(x^*\),计算机通过迭代产生以下序列: \[ x_0\rightarrow x_1\rightarrow x_2\rightarrow\dots\rightarrow x_n\rightarrow\dots \] 只须: \[ \lim_{n\rightarrow\infty}x_n=x^* \] 这便是迭代的思想,迭代的思想在计算机中使用非常广泛。
收敛速度
用迭代思想写算法前,必须考虑的一个因素就是收敛速度。为了衡量算法收敛的速度我们定义p阶收敛:
数列p阶收敛
设\(\lim\limits_{n\rightarrow\infty}x_n=x^*\),若存在\(a>0, p\geq0\)使得 \[ \lim\limits_{n\rightarrow\infty}\frac{|x_{n+1}-x^*|}{|x_n-x^*|^p}=a \] 则称数列\(\{x_n\}\)为p阶收敛,特别的有:
收敛阶\(p=1(a<1)\)时,称为线性收敛;
收敛阶\(p>1\)时,称为超线性收敛;
收敛阶\(p=2\)时,称为平方收敛;
序列收敛阶数越高,则收敛速度越快。
收敛的速度也可以用导数来判断,导数和收敛速度的关系如下所示,如果要证明,只需将函数的泰勒展开写出来,带入p阶收敛的定义即可:
定理
设\(x^*\)是\(\varphi(x)\)的不动点,且 \[ \varphi'(x^*) = \varphi''(x^*) = \dots = \varphi^{(p-1)}(x^*) = 0\qquad(\varphi^{(p)}(x^*) \neq0 ) \] 则\(x_{n+1}=\varphi(x_n)\) p阶收敛
二分法
二分法就是通过判断两端中点的值是否满足某个条件,从而舍弃另一半的候选区域。具体怎么实现我这里就不展开讲了,视具体情况而定,是一个比较常见且简单的算法。二分法每次可以降低函数一半的误差,关于二分法,有以下定理:
定理
设\(x^*\)是\(f(x)=0\)在\([a_0,b_0]\)内的唯一根,且\(f(a_0)f(b_0)<0\),则二分过程中,各区间的中点数列 \[ x_n=\frac{1}{2}(a_n+b_n)(n=0,1,2,\dots) \] 满足 \[ |x_n-x^*|\leq\frac{(b_0-a_0)}{2^{n+1}} \]
也就是说,如果我们想要最终计算的误差小于\(0.5\times 10^{-3}\),只需: \[ \frac{b_0-a_0}{2^{n+1}}\leq 0.5\times 10^{-3} \] 通常,我们把能容忍的误差称为tolerance(容差),如果要满足终止准则,即\(|x_n-x^*|\leq tolerance\),需要的迭代次数为: \[ n\geq\log_2\frac{b_0-a_0}{tolerance} \]
不动点迭代
虽然很多人刚开始没听说过这个词,但如果在了解过该算法后,再去接触其他算法,就会惊奇的发现好多算法的思想和不动点迭代完全一致。
首先,我们看一个表达式: \[ x=(1+x)^{\frac{1}{2}} \] 这个表达式在数学上,表示一个方程,其解约为\(1.618\);在程序员眼中,这也可以是一个赋值语句,假如我们给\(x\)随便取一个初值,我这里给100,循环执行这个赋值语句,我们可以得到如下结果:
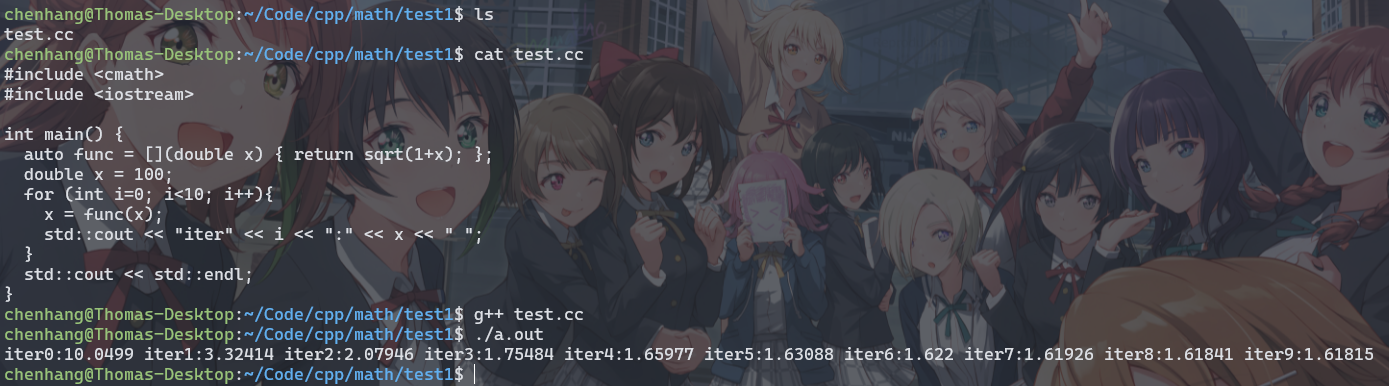
可以看到倒数第二行中,随着迭代次数增加,结果越来越接近\(1.618\),如果循环50次,结果大约为\(1.61803\)。可以看到结果和方程的真值越来越接近。是不是所有的方程都满足上述性质呢?显然不是(比如\(x=x^2\)),不过上述性质也不是巧合,我们把上述解方程的过程称为不动点迭代,其基本思想是将非线性方程求解化为一些列显示的函数值计算。接下来,我们引入定义:
不动点迭代 \[ f(x^*)=0\overset{等价变换}{\Longleftrightarrow}x^*=\varphi(x^*)\Longrightarrow x_n=\varphi(x_{n-1}) \] 我们把第二个等式中的\(x^*\)称为不动点,如果数列\({x_n}\)有极限\(x^*=\lim\limits_{n\rightarrow \infty}x_n\),则称迭代是收敛的。
tips:最简单的不动点就是在\(f(x^*)=0\)两边同时加\(x^*\),得到\(x^*=f(x^*)+x^*\)
不同的不动点在迭代时往往表现出来不同的特性,有些不动点不收敛,有些不动点收敛慢。我们该如何判断呢,显然,这些问题早已被前辈们解决,我们只需要知道其定理,并拿来应用即可。
引理一
如果\(\varphi(x)\)在\([a, b]\)上具有连续的一阶导数,满足:
- \(a\leq\varphi(x)\leq b\)
- 对任意的\(x\in(a,b)\)有\(|\varphi'(x)|\leq L<1\)
则\(\varphi(x)\)在\([a,b]\)有唯一的不动点\(x^*\)
上述的定理给出了不动点存在的充分条件,可以通过上述引理来判断一些函数是否有不动点。接下来,我们引入全局收敛性定理:
定理一(全局收敛性定理)
如果\(\varphi(x)\)在\([a, b]\)上具有连续的一阶导数,满足:
- \(a\leq\varphi(x)\leq b\)
- 对任意的\(x\in(a,b)\)有\(|\varphi'(x)|\leq L<1\)
则对任意的\(x_0\in[a,b]\),迭代格式\(x_{n+1}=\varphi(x_n)\)产生的序列\({x_n}\)收敛到不动点\(x^*\),且满足: \[ |x^*-x_n|\leq\frac{L}{1-L}|x_n-x_{n-1}| \]
上述的定理给出了不动点迭代能够收敛的充分条件。重要的是,根据上述定理,在迭代过程中,我们可以知道我们和真值差距的上界,也就是说该定理可以用来当作收敛条件。
局部收敛定理
设\(x^*\)为\(\varphi(x)\)的不动点,\(\varphi'(x)\)在\(x^*\)连续,且\(|\varphi'(x^*)|<1\),则存在\(x^*\)的某个邻域对任意\(x_0\)属于该邻域,迭代格式\(x_{n+1}=\varphi(x_n)\)产生的序列\(\{x_n\}\)收敛到不动点\(x^*\)。
附录-证明
引理一
存在性证明:
当\(a=\varphi(a)\)或\(b=\varphi(b)\)时,显然成立
当\(a<\varphi(a)\)且\(b>\varphi(b)\)时:
令\(\phi(x) = x-\varphi(x)\),有 \[ \phi(a) = a-\varphi(a) < 0\\ \phi(b) = b-\varphi(b) > 0 \] 由于\(\phi(x)\)在\([a, b]\)内连续,且\(\phi(a)\cdot\phi(b)<0\),则\(\exists\ \xi\in(a,b)\)使得\(\phi(\xi)=0\),即\(\xi=\varphi(\xi)\)
唯一性证明:
设在\([a,b]\)内有两个不动点\(x_1^*,x_2^*\),则有 \[ |x_1^*-x_2^*|=|\varphi(x_1^*)-\varphi(x_2^*)|=|\varphi'(\xi)(x_1^*-x_2^*)|=|\varphi'(\xi)|\cdot|x_1^*-x_2^*|<|x_1^*-x_2^*| \] 显然矛盾,则不肯能存在两个或者以上的不动点。
定理一
收敛性
由 \(x_0\in[a,b]\) ,且在 \([a,b]\) 内,有 \(a\leq\varphi(x)\leq b\) ,则 \(x_n\in[a,b]\), 则有: \[ |x_n-x^*|=|\varphi(x_{n-1})-\varphi(x^*)|=|\varphi'(\xi)|\cdot|x_{n-1}-x^*| \] 则有压缩映像: \[ |x_n-x^*|\leq L|x_{n-1}-x^*|\leq L^n|x_0-x^*| \] 则有: \[ \lim\limits_{n\rightarrow\infty}|x_n-x^*|=0 \]
收敛上界 \[ \begin{eqnarray} |x_n-x^*|=|x_n-x_{n+1}+x_{n+1}-x^*|&\leq&|x_n-x_{n+1}|+|x_{n+1}-x^*|\\ ~&=&|\varphi(x_{n-1})-\varphi(x_n)|+|\varphi(x_n)-\varphi(x^*)| \end{eqnarray} \] \[ |x_n-x^*|\leq L|x_{n-1}-x_n|+L|x_n-x^*|\\ \] \[ (1+L)|x_n-x^*|\leq L|x_{n-1}-x_n| \] \[ |x_n-x^*|\leq \frac{L}{(1+L)}|x_{n-1}-x_n| \]
局部收敛性定理
这个比较容易,我不严谨的证明一下:
由函数的连续性易证,\(\exists\ \delta\),使得在邻域\(N^0:|x-x^*|\leq\delta\)中,有\(|\varphi'(x)|<1\)
则有,对于\(\forall x\in N^0\),即\(|x-x^*|\leq\delta\),有\(|\varphi(x)-x^*|=|\varphi(x)-\varphi(x^*)|\leq|x-x^*|\),即\(\varphi(x)\in N^0\)。由全局收敛性定理可知,迭代法对\(\forall x\in N^0\)都收敛









