
介绍高仙的Lifelong SLAM论文,里面也包含这我这段时间对Lifelong的理解。
介绍
某位大佬曾经说过,Lifelong主要解决两个问题:long term和large Scale。实际上,对于工厂环境下的机器人来讲,大部分时候没必要考虑Large Scale,显然高仙机器人所用的扫地机器人也是不需要Large Scale的。所以,论文上主要解决的也是long term上面的问题。
高仙的Lifelong SLAM基于经典的SLAM框架,前端定位建图,后端回环检测优化,在上述经典SLAM框架上引入地图更新模块,即可做到Lifelong SLAM。可以发现,和经典SLAM框架的区别在于地图更新模块。普通SLAM会将前端建的地图全部加入全局地图,进行回环检测和优化,而引入地图更新的SLAM,在加入的同时也会检测是否要删除全局地图中的部分子图,从而进行裁剪保证SLAM不会随时间而变大。
而Lifelong SLAM最重要的就在于地图更新的策略,这里高仙的论文也是讲解他们的地图更新策略。
要点提炼
- 没有变化判断,直接用新图替换旧图
- 替换时,提取其马尔可夫毯做边缘化
- 对边缘化后的全连接图用周刘树做稀疏化
很显然,高仙这篇论文的核心在于边缘化和稀疏化,边缘化和稀疏化其实也并不是什么新鲜事,Henrik Kretzschmar等人在2011年就提出了用边缘化和稀疏化来保证SLAM运行的Long term,高仙这篇论文在子图框架下重新介绍了一遍这种方法。
系统介绍
本来是不打算按论文结构介绍的,第一次写论文介绍,没有经验,不过按论文结构介绍好像也能够讲清楚🥺
整体介绍
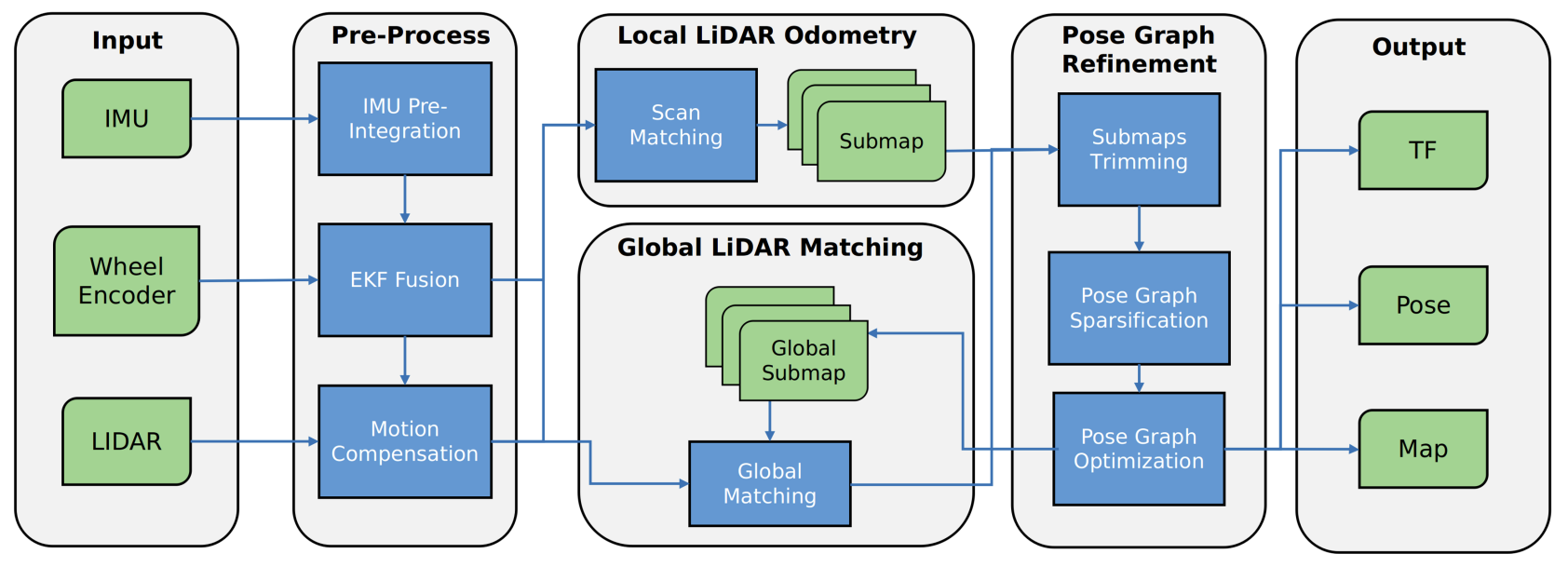
系统的结构如图所示,可以看到由4个模块构成,其中3个模块都是当前SLAM的通用框架:Pre-Process为预处理,负责得到先验预测位姿;Local LiDAR Odometry为雷达里程计,负责建图和定位;Global LiDAR Matching为后端,负责回环检测和优化。而最后一个模块Pose Graph Refinement为更新模块,负责子图修剪(边缘化)、稀疏化、优化,也就是这篇论文的核心模块。
问题模型
作者将SLAM问题建模为多Session下位姿图的优化问题,所谓的Session可以类比为cartographer下的多轨迹,作者这里的一个Session相当于一天,每个Session都有自己的节点、子图、约束,不同Session间联合优化,优化问题可以看作: \[ \mathcal{X}^*,\mathcal{M}^*=\arg\min_{\mathcal{X},\mathcal{M}}J(\mathcal{X}, \mathcal{M}, \mathcal{Z}) \] 其中\(\mathcal{X},\mathcal{M}\)为节点集合和子图集合,\(J\)为代价函数,在本问题中建模为: \[ \begin{eqnarray} J(\mathcal{X}, \mathcal{M}, \mathcal{Z})&=&\left\|x_0^0\right\|_{\Omega_0}+\left\|m^0_0\right\|_{\Omega_0}\\ &+&\sum_{s=0}^{S-1}(\sum_{i,j}\left\|x_i^s\ominus m_j^{s'}\ominus z^{mix}_{i^s,j^{s'}}\right\|^2_{\Omega^{mix}_{i^s,j^{s'}}}\\ &+&\sum_{i,j}\left\|x_i^s\ominus x_j^{s'}\ominus z^{odom}_{i^s,j^{s'}}\right\|^2_{\Omega^{odom}_{i^s,j^{s'}}}\\ &+&\sum_{i,j}\left\|x_i^s\ominus x_j^{s'}\ominus z^{node}_{i^s,j^{s'}}\right\|^2_{\Omega^{node}_{i^s,j^{s'}}}\\ &+&\sum_{i,j}\left\|m_i^s\ominus m_j^{s'}\ominus z^{map}_{i^s,j^{s'}}\right\|^2_{\Omega^{map}_{i^s,j^{s'}}}) \end{eqnarray} \]
表达式中:\(x\)表示节点;\(m\)表示地图;\(z\)表示观测;节点中右上标表示Session ID,右下标表示节点ID;观测量的右上角表示类型,右下角表示哪两个节点间的观测;表达式中的范数为: \[ \left\|e\right\|_\Omega=e^T\times\Omega\times e \] 式中第1行为固定点,应该不用管。第二行为回环检测的约束。第三行为激光里程计的约束。第四行为节点间约束,应该是由边缘化产生。第5行为子图间约束,应该由边缘化产生。这样就能将改表达式理清了。
这里所说的节点有时候代表激光关键帧,有时候代表激光关键帧+子图节点。读者(如果有的话🥺)根据实际情况注意区分,应该还是很好理解的。
PGR
这里开始就到了论文的核心模块,作者将其分为Multi-session Localization和Pose Graph Refinement两部分进行介绍,我这里和作者保持一致。
Multi-session Localizaiton
个人感觉这部分的目的在于地图的保存,如果真要做到Lifelong SLAM的话,似乎要不要分Session都无所谓?这一步在我看来似乎有点多余了,当然有可能作者是受到了cartographer轨迹思想的影响。
作者这里使用Session的机制管理节点和子图(类似于Cartographer中的轨迹)。Session 0利用传感器数据构建全局栅格地图,地图由前端构建,每个子图由固定个数的关键帧构成,后端回环检测加优化。
定位从Session 1开始,构建好一个子图后送到PGR进行更新,同时,回环检测的结果也送入PGR。PGR负责接收新子图和约束,进行子图裁剪、位姿图稀疏化、位姿图优化。整体的流程如下图所示:
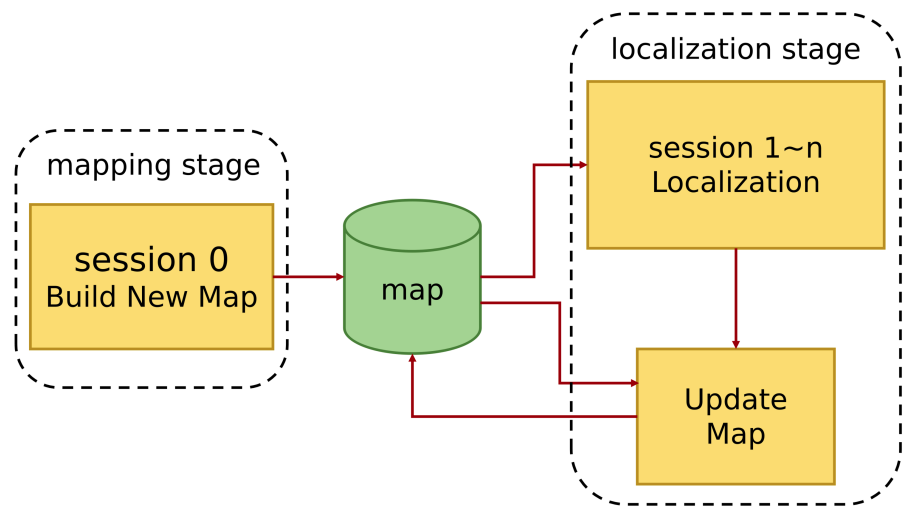
这里有个关键点:Session 0是不参与更新的,图中其实也可以看出来,不过作者只在后续的实验部分提到了。
Pose Graph Refinement
PGR可以翻译成位姿图改进(大概,也许?),他主要的功能就是子图裁剪、稀疏化、优化,前面已经多次提到,这里将分模块介绍。首先,我们可以从图片上略知一二。
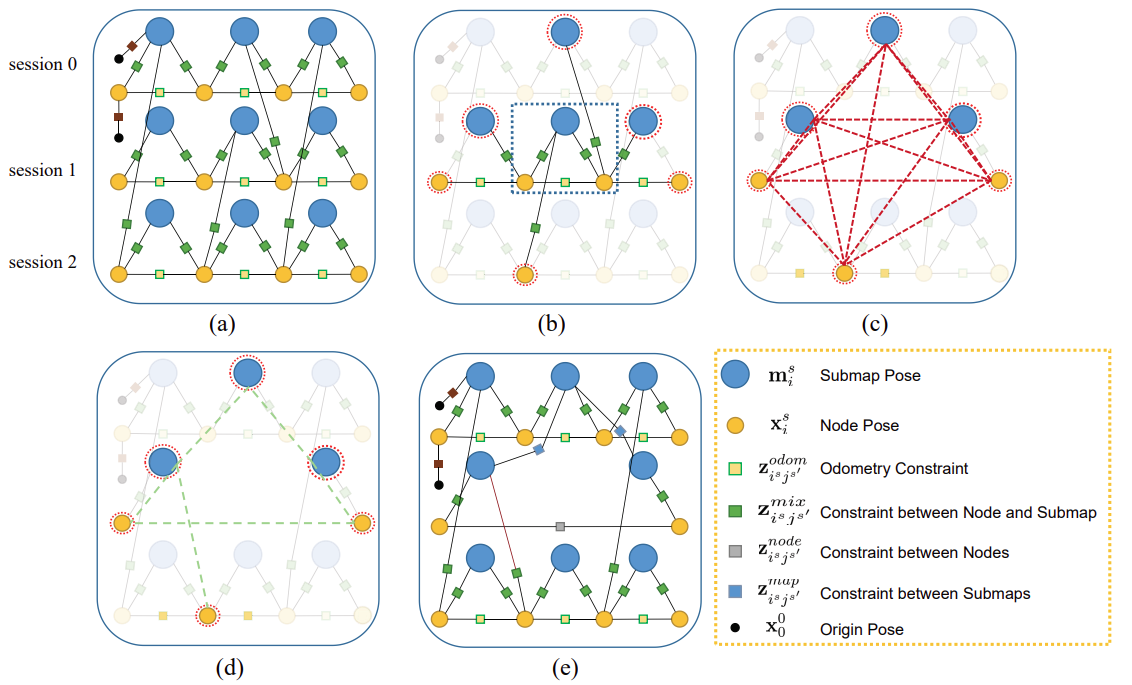
如上图所示:图中每个子图有两个节点构成(实际中不可能这么少);这里删除Session 1的一个子图,如图b所示;通过边缘化删除后,会将位姿图变稠密,如图c;通过周刘树进行稀疏化后可以得到图d;最后结果如图e所示。
- 子图裁剪
当机器人重新进入之前进入过的区域时,进行子图裁剪,核心思量就是:通过修剪旧子图,限制子图数量。区别于通过探测环境变化再修剪,作者这里采用交叠比例的方法来修剪子图,如果交叠比例大于某个值,就把该子图标记为要修剪得子图。在另一方面新子图的加入是不考虑旧子图的删除的,这种方法能够保证在固定区域内计算的复杂度一致。
- 位姿图稀疏化
如果采用cartographer那样,直接丢弃子图,会使位姿图丢失很多信息,导致位姿图不稳定。边缘化是缓解该问题的有效方法,但是边缘化却会引入稠密填充(Dense
fill-in),如上图c所示,会使计算复杂度上升。作者这里说他们使用周刘树近似独立消除团,这个过程用概率图模型可以表示如下:
\[
\begin{eqnarray}
p(x_1,...,x_n)&=&p(x_1)\prod_{i=2}^n{p(x_i|x_{i-1},...,x_1)} \\
&\approx&p(x_1)\prod_{i=2}^n{p(x_i|x_{i-1})}\\
&=&q(x_1,...,x_n)
\end{eqnarray}
\]
上述表达式第二行的近似原则是,使得KL散度最小,也就是使得下述表达式最小:
\[
D_{KL}(p||q)=\int_x{p(x)\log{\frac{p(x)}{q(x)}dx}}
\]
得到近似的消除团后,将其合并回原始的位姿图(之前的被删除掉了)。作者在处理消除团时,将所有节点(子图、关键帧)当成相同对象进行处理,所以在处理后会引入node-to-node以及submap-to-submap这类约束。
最开始我对上述的一些概念不太了解,所以说目前还是知识太欠缺了,下面是经过一段学习后对其中一些知识的理解,这里只简单介绍,后续可能单独开博客进行详细介绍
概率图模型:将概率分布中的变量,比如\(p(x_1,...,x_n)\)中的\(x_1,...,x_n\)看作节点,他们之间如果有依赖关系就看作边,最后用图画出来的模型叫做概率图模型,用概率图模型表示概率分布可以引入计算机图中的一些方法对概率分布进行处理。概率图模型分为有向图模型(贝叶斯网络)和无向图模型(高斯马尔可夫随机场),贝叶斯网络可以很直观的写出其概率分布,马尔科夫随机场通常通过势函数来表示其分布。
团:通常是无向图中的概念,是一个关于节点的集合,节点之间都是连通的。最大团就是添加概率图中其他任何一个变量都不构成团。这里的消除团其实就是一个团,在边缘化过程中会将马尔可夫毯中的变量两两链接,就形成了一个团,通常将其称为消除团。
KL散度:用于衡量两个概率分布的距离。
CLT:对于周刘树,要学明白太难了,不过我再其他论文中看到,在无向图模型中,一个集合的周刘树等于其Kruskal算法的结果(这就是概率引入图的好处吧,虽然不知道原理,但看到Kruskal算法立马能够编写代码,感谢前人的智慧😭)。
- 优化
优化这里就不多介绍了,就是直接将结果全局优化一次,优化的函数前面模型中有介绍,作者使用的是Google的Ceres优化库进行优化求解。
最后,作者给出了算法的伪代码,如下所示,流程比较简单,一眼就能看明白,复杂点在于函数内部的实现:

总结
可以看出,这篇论文好像讲了很多,但又好像什么都没讲,如果基础知识不够,看了等于没看😭。不过对于入门Long term的思量还是很有帮助的,后面我我将继续跟进其中的一些原理。









