学习下大佬们对高斯牛顿法在实际中的应用o(￣▽￣)ブ

简介

LIO-SAM中，大部分代码都比较好理解，稍微有点麻烦的就是LMOptimization，表面上说是LM优化，但这里其实用的是高斯牛顿优化（优化相关的方法后面会另开博客讲解）。

LM优化相关的原理后面会另开优化博客讲解，这里主要是相当于一个LM优化的应用吧。

推导

下面的推导是我参考一些博客和书籍自己推了一遍，如果看到有错误的地方欢迎指出~

对于任何一个优化方法，优化前都需要构建其误差函数，这里的误差函数由点到面的距离构成，表达式如下所示： \[ \arg\min_{^M_LT}\left\|f(^M_LT)\right\|^2_2=\arg\min_{^M_LT}\left\|\sum_is_i\left\{(\overrightarrow{n}_i)^Tz_i+D_i\right\}\right\|^2_2=\arg\min_{^M_LT}\left\|\sum_is_ie_i\right\|^2_2 \] 其中\(z_i\)为点云在地图的位姿，\(\overrightarrow{n}_i=[A,B,C]^T\)为\(z_i\)点云所匹配平面的法向量，\(^M_LT\)为Lidar在Map中的位姿，也就是要优化的变量。这里平面方程如下所示，很容易理解，上面的误差函数就是每个点到面的距离加权。 \[ Ax+By+Cz+D=0 \] 然后就是\(z_i\)的计算，优化变量也存在\(z_i\)里面，设\(\tilde{z}_i\)为点云在Lidar坐标系下的位姿，那么\(z_i\)的计算公式如下所示： \[ z_i=^{M}_{L}T\times\tilde{z}_i=^M_LR\times\tilde{z}_i+^MP_L \] 其中\(^M_LR\)为Map下Lidar的姿态，可以用欧拉角计算（欧拉角只有3个变量方便优化？），众所周知机器人欧拉角一般使用rpy角（可以参考我之前一篇博客）。在LIO-SAM中，这里先将Lidar坐标系转化为相机坐标系，对应关系如下所示：

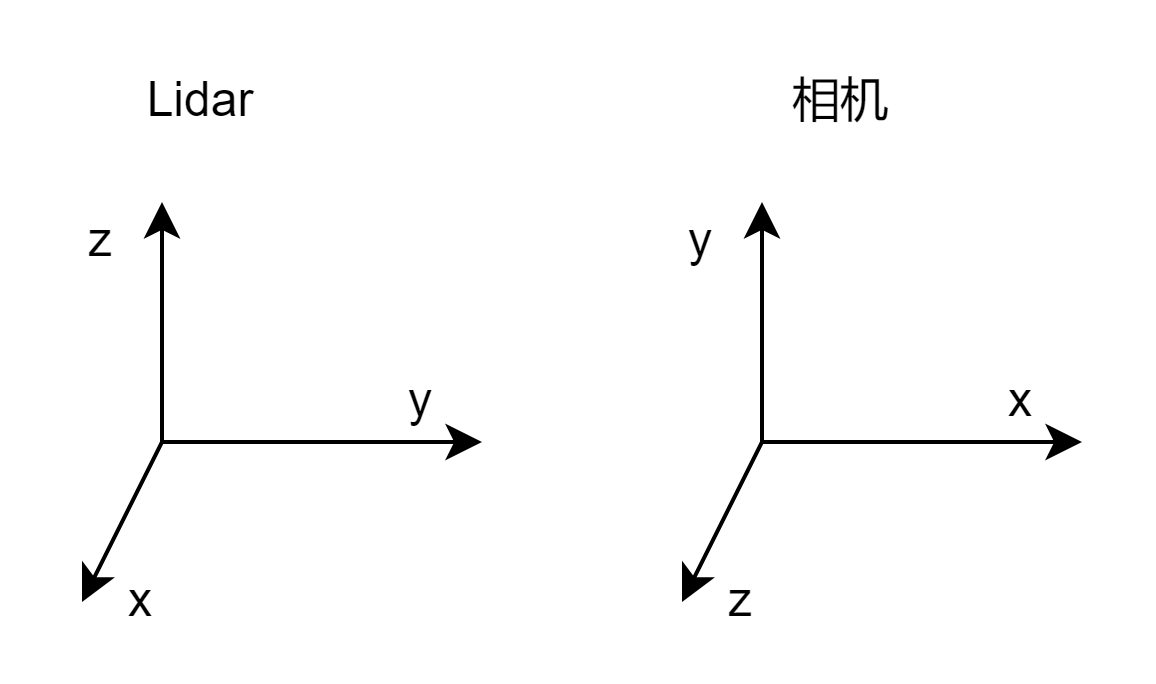
根据图像可以得到其平移：x->z，y->x，z->y

其旋转的yaw角（Lidar下为rz）：rz->ry（其他角同理）

我这里直接使用Lidar坐标系推导，不做变换（变换的可以参考这篇博客)。那么可以得到\(^M_LR\)的计算公式如下（这里简写成\(R\)）： \[ \begin{eqnarray} R&=&R_y\times R_p\times R_r=R_{rz}\times R_{ry}\times R_{rx} \nonumber \\ ~&=&\begin{aligned}\begin{bmatrix} crz\cdot cry&-srz\cdot crx+crz\cdot sry\cdot srx&srz\cdot srx+crz\cdot sry\cdot crx \nonumber \\ srz\cdot cry&crz\cdot crx+srz\cdot sry\cdot srx&-crz\cdot srx+srz\cdot sry\cdot crx \nonumber \\ -sry&cry\cdot srx&cry\cdot crx \nonumber \end{bmatrix}\end{aligned} \nonumber \end{eqnarray} \] 然后就是求雅可比矩阵，根据优化的变量，雅可比矩阵如下所示： \[ J=\frac{\partial{f(^M_LT)}}{\partial^M_LT}=\left[\frac{\partial e}{\partial rx},\frac{\partial e}{\partial ry},\frac{\partial e}{\partial rz},\frac{\partial e}{\partial x},\frac{\partial e}{\partial y},\frac{\partial e}{\partial z}\right]^T \] 对于求和的雅可比矩阵，我们通常看单个变量\(e_i\)，再对其求和，对于单个变量，首先给出对角度\(rx\)的偏导： \[ \begin{eqnarray} \frac{\partial e_i}{\partial rx}&=&\overrightarrow{n}_i^T\cdot\frac{\partial z_i}{\partial rx}=\overrightarrow{n}_i^T\cdot\frac{\partial^M_LR}{\partial rx}\cdot\tilde{z}_i \nonumber \\ ~&=&\overrightarrow{n}_i^T\cdot\begin{aligned}\begin{bmatrix} 0&srz\cdot srx+crz\cdot sry\cdot crx&srz\cdot crx-crz\cdot sry\cdot srx \\ 0&-crz\cdot srx+srz\cdot sry\cdot crx&-crz\cdot crx-srz\cdot sry\cdot srx \\ 0&cry\cdot crx&-cry\cdot srx \end{bmatrix}\end{aligned}\cdot\tilde{z}_i \nonumber \end{eqnarray} \] 然后是对平移\(x\)的偏导： \[ \begin{eqnarray} \frac{\partial e_i}{\partial rx}&=&\overrightarrow{n}_i^T\cdot\frac{\partial z_i}{\partial x}=\overrightarrow{n}_i^T\cdot\frac{\partial ^MP_L}{\partial x} \nonumber\\ ~&=&\overrightarrow{n}_i^T\cdot\begin{aligned}\begin{bmatrix} 1 \\0 \\0 \end{bmatrix}\end{aligned} \nonumber \end{eqnarray} \] 其他偏导求法同理，得到了单个变量的偏导，则雅可比矩阵可以求和得到，得到了雅可比矩阵后，即可计算增量： \[ H\Delta x=-g \] \[ J^T(x)J(x)\Delta x=-J^T(x)f(x) \]

计算出\(\Delta x\)后，不断迭代即可求出Lidar到Map的坐标变换，即Lidar的定位。

我这里写的对\(J_i\)求和，实际做时往往是把\(J\)排列成一个矩阵\(J=[J_1,J_2,...J_n]\)，这样\(J^TJ\)其实就相当于进行了一次求和（这种更快？）。

改进

IMU紧耦合

原版的liosam优化到上面就结束了，这里imu并没有采用紧耦合的方式，也就是优化过程中imu并没有提供约束。在实际使用中，某些地方会出现匹配效果不好，定位漂移等情况。为了解决上述问题，我这里根据自己的理解尝试添加imu约束，也就是紧耦合的方式。

添加imu约束前，需要考虑一下使用imu提供的什么约束。很显然，imu提供的约束只有姿态比较准确（高精度的imu），适合作为约束加到优化函数中去。

将imu作为约束加入优化函数中，可以得到优化函数的表达式： \[ \arg\min_{^M_LT}\left\|f(^M_LT)\right\|^2_2=\arg\min_{^M_LT}\left\|\sum_is_ie_i+\left\|R_p-^M_LR\right\|^2_\Omega \right\|^2_2 \] 其中\(R_p\)为imu相对于上次姿态变化量预测出来的姿态，\(^M_LR\)为优化变量中的旋转部分，这里两个变量都为\(3\times1\)向量，即rpy。将其展开可得： \[ \left\|R_p-^M_LR)\right\|^2_\Omega=\Omega_1\cdot(rx_p-rx)^2+\Omega_2\cdot(ry_p-ry)^2+\Omega_3\cdot(rz_p-rz)^2 \]

其雅可比矩阵可以写作： \[ J=\frac{\partial{f(^M_LT)}}{\partial^M_LT}=\frac{\partial\left(f_1(^M_LT)+f_2(^M_LT)\right)}{\partial^M_LT}=J_{f1}+J_{f2} \] 其中，\(J_{f1}\)为点到面距离的残差部分得到，和上面推导一样，这里不再展开重新推导。\(J_{f2}\)为imu约束残差得到，显然，平移部分偏导为0，只有旋转，可以得到如下表达式： \[ J_{f2}=\frac{\partial f_2(^M_LT)}{\partial^M_LT}=\left[\frac{\partial f_2}{\partial rx},\frac{\partial f_2}{\partial ry},\frac{\partial f_2}{\partial rz},0,0,0\right]^T \] 这里的偏导很简单，我这里给出\(\frac{\partial f_2}{\partial rx}\)的计算，其他同理： \[ \frac{\partial f_2}{\partial rx}=2\cdot\Omega_1\cdot(rx-rx_p) \] 然后使用高斯牛顿迭代法不断迭代就可以得到最优解。

求和和上面一样，这里为了方便，可以直接在上面所排列的矩阵\(J=[J_1,J_2,...J_n]\)后面再添加一个残差项\(J=[J_1,J_2,...,J_n,J_f2]\)，同理\(f(x)\)也添加一列，就可以简单的将残差添加到前面的表达式中了。

融合重力对齐

还可以使用重力向量试试，即优化出来的姿态可以得到一个重力向量，IMU可以得到一个重力向量，两个之间差值作为残差加入优化。也就是添加一个： \[ f_3=\left\|^m_IR\times \begin{bmatrix}0&0&1\end{bmatrix}^T-\mathbf{a}\right\|^2_\Omega=\left\|R\times^I_LR\times\begin{bmatrix}0&0&1\end{bmatrix}^T-\mathbf{a}\right\|^2_\Omega=\left\|\mathbf{\tilde{a}}-\mathbf{a}\right\|^2_\Omega \] 展开后为： \[ \Omega_1\left(\tilde{a}[0]-a[0]\right)^2+\Omega_2\left(\tilde{a}[1]-a[1]\right)^2+\Omega_3\left(\tilde{a}[2]-a[2]\right)^2 \] 我们将上面的R带入，可以得到\(\mathbf{\tilde{a}}\)的表达式： \[ \mathbf{\tilde{a}}= \begin{bmatrix}crz\cdot cry\cdot^I_LR[0][2]+\left(-srz\cdot crx+crz\cdot sry\cdot srx\right)\cdot^I_LR[1][2]+\left(srz\cdot srx+crz\cdot sry\cdot crx\right)\cdot^I_LR[2][2]\\ srz\cdot cry\cdot^I_LR[0][2]+\left(crz\cdot crx-srz\cdot sry\cdot srx\right)\cdot^I_LR[1][2]+\left(-crz\cdot srx+srz\cdot sry\cdot crx\right)\cdot^I_LR[2][2] \\ -sry\cdot^I_LR[0][2]+cry\cdot srx\cdot^I_LR[1][2]+cry\cdot crx\cdot^I_LR[2][2] \end{bmatrix} \] 对原式求偏导可以得到\(J_{f3}\)，老规矩，我这里也只求一个： \[ \frac{\partial f_3}{\partial rx}=2\cdot\Omega_1\cdot\left(\tilde{a}[0]-a[0]\right)\cdot\frac{\partial \tilde{a}[0]}{\partial rx}+2\cdot\Omega_2\cdot\left(\tilde{a}[1]-a[1]\right)\cdot\frac{\partial \tilde{a}[1]}{\partial rx}+2\cdot\Omega_3\cdot\left(\tilde{a}[2]-a[2]\right)\cdot\frac{\partial \tilde{a}[2]}{\partial rx} \] 这里求导写出来比较大，原理很简单，我就不在这里写下来了，毕竟还需要根据实际应用重新计算😭。