110025601_p0

这篇博客太枯燥了，不想写，放一张yui的照片缓解枯燥吧😊

机器人的位姿

其实这篇博客要讲清楚最好结合图片讲解，但作者目前没有合适的画3D坐标系的工具，所以这里很多关系都是用文字的描述。这里还缺少部分的数学推导，如有需要的朋友可以看机器人学导论的第二章（个人感觉讲的比视觉SLAM14讲清楚）。

我们想要了解机器人在空间中的位置，通常给定参考坐标系，以及机器人位置\(x,y,z\)即可。当然，这是不考虑机器人姿态的情况下，通常情况下，如果只知道机器人的位置而不知道姿态，基本无法控制机器人。在2D下，通常用\(x,y,\theta\)来表示机器人的位置加姿态。机器人在空间中具体的位置加姿态通常用位姿来表示。也就是 \[ Pose=Translation+Rotation \] 位置（Translation）表示通常很简单，下面我直接讲解一下姿态的表示。

旋转矩阵

三维下姿态又很多种表示方式，这里先介绍旋转矩阵（最常用），其他的方式在后面介绍。

在三维空间下，为了更直观的理解物体的姿态，我们在机器人身上放一个右手坐标系（三轴正交），便于观察机器人的姿态变换。现在的问题变成了如何表示这个坐标系的姿态。

由于我这里不考虑位置，那么，我直接将坐标系放到原点便于观察。很容易想到，如果分别将三个轴对应的向量写下来，便能唯一表示一个姿态。把这三个轴的坐标（按列向量）写成矩阵，那么它就是旋转矩阵： \[ R=(\overrightarrow{x},\overrightarrow{y},\overrightarrow{z})= \begin{aligned} \begin{bmatrix} x_1 & y_1 & z_1\\ x_2 & y_2 & z_2\\ x_3 & y_3 & z_3 \end{bmatrix} \end{aligned} \] 根据上述旋转矩阵的定义，我们不难发现旋转矩阵的几个性质：

旋转矩阵是正交矩阵
如果\(^A_BR\)表示A参考系下B的旋转矩阵，那么B参考系下A的旋转矩阵为：\(^B_AR=^A_BR^T\)

对于上述第二个性质，如果要证明的话，可以将R矩阵写做内积形式，比如\(x_1=X_A\cdot X_B=|X_A|\cdot|X_B|\cos<X_A,X_B>\)，也就是坐标系B在坐标系A下的投影。如果将矩阵中所有元素写成上述形式，可以发现矩阵的行向量为B在A坐标系下\(\overrightarrow{x},\overrightarrow{y},\overrightarrow{z}\)的投影，也即性质2所表达的内容。

顺便补充一下，二维右手坐标系下\(\theta\)角姿态对应的旋转矩阵为： \[ R= \begin{aligned} \begin{bmatrix} cos\theta & -sin\theta\\ sin\theta & cos\theta\\ \end{bmatrix} \end{aligned} \]

对应的，绕z轴旋转\(\theta\)对应的矩阵为： \[ R=\begin{aligned} \begin{bmatrix} cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0\\ 0&0&1 \end{bmatrix} \end{aligned} \]

位姿

知道了旋转的表示，我们就可以表示机器人的位姿了。通常情况下，我们把坐标系写在左边，参考坐标系写在左上，而原点写在右下角。比如，我们要表示A坐标系下，B的位姿，就可以： \[ \left\{^A_BR,^AP_{BORG}\right\} \] 其中\(^A_BR\)表示B的姿态，\(^AP_{BORG}\)表示B原点的坐标。

这样的表示在计算时会带来很大的方便，后面将映射的时候就能体会到了，学会这种表达后，坐标变换有手就行😎

映射

这里有些地方也叫坐标变换，以前我刚学的时候，总是把算子和映射混着用，虽然很多时候表达式通用，但最好还是区分一下。后面的介绍中，注意区分点和坐标系，点是不带姿态的，坐标系是带姿态的，两者搞混淆后阅读起来就不知所云了。

很多时候，我们想要在不同坐标系下表达同一个东西，比如知道小车在里程计坐标系下的位姿，想要得到小车在全局地图坐标系下的位姿，就涉及到坐标的转换，可以说是经常需要用到的。

对于只有平移的映射，我们可以直接用矢量相加的方法求某个点的坐标，比如，已知P点在B坐标系下的坐标，以及A坐标系在B坐标系下的坐标，求P点在A坐标系下的坐标就可以： \[ ^AP=^BP+^AP_{BORG} \] 而对于只有旋转，即已知P点在B坐标系下的坐标，以及B坐标系在A坐标系下的旋转，那么我们可以得到点在A坐标系下的旋转： \[ ^AP=^A_BR^BP \]

上述表达式通过线性代数的知识很好理解，由于\(^A_BR\)的列向量是B坐标系的基向量，上述表达式就是一个坐标变换公式： \[ ^AP=(\overrightarrow{e_1},\overrightarrow{e_2},\overrightarrow{e_3})\times\begin{aligned}\begin{bmatrix}x\\y\\z\end{bmatrix}\end{aligned}=x\cdot\overrightarrow{e_1}+y\cdot\overrightarrow{e_2}+z\cdot\overrightarrow{e_3} \] 而对于既有旋转又有平移的变换，要计算B坐标系下的P点在A坐标系下的坐标，我们可以将其分两步：首先通过坐标变换，得到和A相同姿态的A'坐标系下P点的坐标，这时候A'坐标系和B坐标系只有平移关系了，再通过平移得到P再B坐标系下的坐标。即： \[ ^AP=^A_BR^BP+^AP_{BORG} \]

上述计算虽然直观，但是在推导表达式时，有时候面对连续多个变换（A到B再到C再到D），如果还用上述变换的方式，写出来的表达式非常复杂，于是人们引入一种叫齐次变换矩阵的概念，其定义如下： \[ ^A_BT=\left[\begin{array}{ccc:c} &^A_BR&&^AP_{BORG}\\ \hdashline0&0&0&1 \end{array}\right] \]

有了其次变换矩阵，我们可以将坐标变换写成矩阵形式： \[ \left[\begin{array}{1}^AP\\1\end{array}\right]=^A_BT^BP=\left[\begin{array}{ccc:c} &^A_BR&&^AP_{BORG}\\ \hdashline0&0&0&1 \end{array}\right]\left[\begin{matrix}^BP\\1\end{matrix}\right] \] >这里面最右边再坐标底下再加一个1的坐标叫做齐次坐标，有时候他和普通坐标会混用，需要根据矩阵自行考虑是否加1

这时候对于多个变换，我们就会惊奇的发现，其上下标消除的特点，比如将C坐标系下的点P变换到B坐标系下，再变换到A坐标系下，就有： \[ ^AP=^A_BT^B_CT^CP \] 由于\(^A_BT\)和\(^B_CT\)都是\((4\times4)\)的矩阵，根据矩阵相乘的结合律，我们可以将其合在一起，而合在一起的这个变换显然直接表示了坐标系C到A的齐次变换矩阵，即： \[ ^A_CT=^A_BT^B_CT=\left[\begin{array}{ccc:c} &^A_BR^B_CR&&^A_BR^BP_{CORG}+{^A}P_{BORG}\\ \hdashline0&0&0&1 \end{array}\right] \] 我们发现，这个过程有点像左边左下角的角标把右上角的角标消掉了，在实际计算各个坐标变换时，我们常用这种方法来帮助理解和简化计算，是不是非常方便😊。对于其次变换矩阵，其逆虽然不再等于转置，但也有快速计算方法： \[ ^B_AT=^A_BT^{-1}=\left[\begin{array}{ccc:c} &^A_BR^{T}&&-^A_BR^T\times{^A}P_{BORG}\\ \hdashline0&0&0&1 \end{array}\right] \]

算子

简单理解，映射就是一个物体在不同坐标系之间转换，而算子就是在同一个坐标系下，将P点移动到P'点的变换矩阵。

有时候我们要移动一个点，比如让激光点云旋转10°，或者让激光点云向前平移10cm，这时候怎么做呢？这样的操作和变换有什么关系呢？直接说结论：包含旋转R和平移Q的变换与描述某个坐标系旋转R并平移Q的变换是相同的。

首先考虑简单的平移，将点P向前移动\(x\)，其移动后的坐标为： \[ P'=P+\begin{bmatrix}x\\0\\0\end{bmatrix} \] 显然，这和坐标系B在坐标系A前面\(x\)的平移变换是一致的。

然后考虑旋转，将P点绕Z轴旋转\(\theta\)，那么旋转后的P点位置如何计算呢？我们可以使用映射的方法计算，思考一下，如果将P点绕Z轴旋转\(\theta\)，就相当于把坐标轴旋转\(-\theta\)，假设原始坐标系是A，旋转后新坐标系为B，那么我们就可以将上述过程转化为计算B坐标下P点的坐标，首先计算旋转矩阵\(^B_AR\)，即B为参考坐标系下A坐标系的姿态： \[ ^B_AR=\begin{aligned} \begin{bmatrix} cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0\\ 0&0&1 \end{bmatrix} \end{aligned} \] 可以得到旋转\(\theta\)后P点的坐标为： \[ P'=R\times P=^B_AR\times P \] 也就是说，旋转也满足上述结论，将旋转和平移结合一下，那么就可以得到我最开始得到的结论🫡

绕固定轴旋转

绕一个固定轴旋转的旋转矩阵经常使用，我这里记录一下绕不同轴旋转得到的矩阵（实际上根据旋转矩阵的定义也能很快确定），方便后面参考使用。

下面的表达式中使用简写\(crx\)代表\(\cos(\theta_x)\)，也就是x轴方向旋转\(\theta_x\)的\(\cos\)值，\(srx\)同理。

绕x轴旋转得到的旋转矩阵： \[ R_{rx}= \begin{aligned} \begin{bmatrix} 1&0&0\\0&crx&-srx\\0&srx&crx \end{bmatrix} \end{aligned} \] 绕y轴旋转得到的旋转矩阵： \[ R_{ry}=\begin{aligned}\begin{bmatrix}cry&0&sry\\0&1&0\\-sry&0&cry\end{bmatrix}\end{aligned} \] 绕z轴旋转得到的旋转矩阵： \[ R_{rz}=\begin{aligned}\begin{bmatrix}crz&-srz&0\\srz&crz&0\\0&0&1\end{bmatrix}\end{aligned} \]

欧拉角和旋转向量

上面讲了这么多，相信大家都觉得挺简单的，自己映像中好像没这么简单吧(・∀・(・∀・(・∀・*)，印象中好像还有什么左手坐标系，右手坐标系、雷达坐标系、相机坐标系、内旋、外旋、X-Y-Z、rpy...什么的。这部分可以说是新手的噩梦😰，让人闻风丧胆。不过不要担心，某奥里给曾经说过，战胜恐惧的最好办法就是面对恐惧，干就完了，奥里给！！！！

学会了上一章节，相信代码中的各种变换能轻而易举的看懂，毕竟不管是Eigen库还是ros的tf库，其都支持上述的乘法形式的坐标变换，但很多时候，我们为了图方便并不喜欢用矩阵来表达姿态。比如有人问你相机姿态是多少，相信没人想听别人说出一个旋转矩阵。而欧拉角就解决了这一痛点。当然，四元数是解决了欧拉角的痛点。

坐标系

首先，要声明一点的就是，坐标系放在这里讲，表明上述的旋转矩阵在所有坐标系下都是通用的。不管坐标系是左手，右手，x轴朝前等等，绕z轴得到的旋转矩阵都是上面所提到的旋转矩阵，不过由于坐标系的定义不同，旋转出来的物理（实际）效果可能完全不同。

坐标系这里放一小章讲并不是因为它内容多，而是因为它很容易让新手（比如当初的我）混淆。这里介绍一些常用的坐标系：

左/右手坐标系

左右手坐标系的定义如下图所示，大拇指指向z轴，其余四指由x轴握向y轴，哪只手成功即为对应的坐标系：

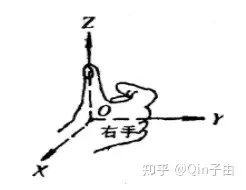
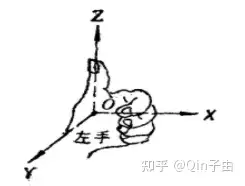
Lidar坐标系

Lidar坐标系一般如下图所示，即x轴朝前的右手坐标系：

相机坐标系

相机坐标系一般如下图所示，即z轴朝前的右手坐标系：

这里所谓的超前就是正放，比如雷达正放和相机正放。

Lidar坐标系转相机坐标系

很显然，由上面可知，Lidar坐标系和相机坐标系是不一样的，如果两个传感器都正放在车上，要对Lidar和相机的参数做联合优化时，往往需要把Lidar坐标系转换到相机坐标系，根据上图关系可以知道，如果一个点云的坐标为\((x,y,z)\)，那么将他转化到相机坐标系，他的坐标为\((y,z,x)\)。

同时，绕不同轴转的角度也需要对应的转换，比如绕x轴转rx，对应到相机坐标系为绕z轴转rx。这里需要结合后面欧拉角看。

欧拉角

这部分非常绕，我下面讲解的东西虽然在某些情况下好像能用，但是换一个环境好像又对不上了，感觉不同的教材，不同的软件定义不同，使用时还是要注意以下，不过大体上是对的

欧拉角的思想很简单，将空间中任意一个姿态分解成3个顺序旋转（也就是说按照规则转3次后得到姿态）。这样就可以用3个变量表示空间中任意姿态了。根据旋转的规则不同，欧拉角的值也有所不同。由于欧拉角按顺序旋转，旋转的方式有很多种，可以按下分类：

绕固定轴旋转（外旋）：X-Y-Z，Z-X-Y...
绕旋转后的轴旋转（内旋）：X-Y-Z，Z-X-Y...

举个例子，Z-Y-X外旋，就是先绕Z轴转，再绕Y轴转，最后X轴转，这里面的xyz轴是固定的。而Z-Y-X内旋就是绕Z轴转后，绕旋转后坐标系的Y轴转下一次。朋友们可以拿身边的物体试一下，这两种转法是不一样的。通常情况下，绕固定轴旋转，每次旋转都是左乘旋转矩阵，这点和我们之前讲的算子一样，比如绕Z轴转\(R_z\)，再绕Y轴旋转\(R_y\)，最后绕X轴旋转\(R_x\)，其旋转矩阵为： \[ R=R_x\times R_y\times R_z \] 而内旋都是右乘旋转矩阵，所以内旋Z-Y-X和外旋X-Y-Z得到的旋转矩阵相同（也可以自己用物体试验一下，真是难以理解呢，太神奇了）。上述的旋转顺序如果是内旋，得到的旋转矩阵为： \[ R=R_z\times R_y\times R_x \] 对于不同的旋转方式，所对应的运算也不相同。为了便于讨论，在机器人领域中，我们常用rpy角，rpy角是一种特殊的欧拉角，其规则为：旋转顺序：Y-P-R，或则说是Z-Y-X（不一定？跟坐标系定义有关），绕旋转后的轴旋转（内旋）。我这里参考的是视觉SLAM14讲上的定义，同时，我注意到网上有很多跟其定义的不一样，使用时注意区分。

需要注意的是，机器人领域中的rpy角一般是指在Lidar坐标系下的旋转，如果是相机坐标系下，旋转顺序需要做一定的转化。

rpy角和旋转矩阵的转换方式如下（我这里的zyx是对应于lidar的，相当于z在上x向前的右手坐标系，对于不同的坐标系得到的结果也不同） \[ \begin{eqnarray} R&=&R_{yaw}\times R_{pitch}\times R_{roll}=R_{rz}\times R_{ry}\times R_{rx}\\ &=&\begin{bmatrix}crz\cdot cry&-srz\cdot crx+crz\cdot sry\cdot srx&srz\cdot srx+crz\cdot sry\cdot crx\\srz\cdot cry&crz\cdot crx+srz\cdot sry\cdot srx&-crz\cdot srx+srz\cdot sry\cdot crx\\-sry&cry\cdot srx&cry\cdot crx\end{bmatrix}\end{eqnarray} \]

对于不同坐标系，比如相机坐标系（z朝前的右手坐标系），yaw角对应的就是\(R_{ry}\)。总之公式前半部分一定是对的，后半部分根据坐标系不同需要注意一下。同时，这里是内旋，所以旋转对应右乘。

到这里，我们就把欧拉角介绍清楚了，虽然表面上把变量从9个减少到了3个，但却更容易混淆了，旋转矩阵只需要给定坐标系、旋转矩阵两个量就能唯一确定一个旋转，而欧拉角需要坐标系、旋转顺序、内旋/外旋、旋转角度才能唯一确定一个旋转，可以说是真让人头大。那么有没有什么方法既可以减少变量，由不容易混淆（没有奇异）呢。下面介绍四元数。 >其实这里还有一个问题，就是如何从旋转矩阵得到欧拉角，做法其实不复杂，根据上述转换关系，通过矩阵内部元素之间的乘除法可以得到对应欧拉角的正弦、余弦、正切值等，然后通过反三角计算即可

旋转向量

旋转向量在求导时经常用到相关概念，以我目前的认知来看，我认为是旋转向量和梯度很像，他既有方向，又有大小，即像内旋一样取决于当前姿态，又没有各种歧义。这部分在后面的李群和李代数中非常有用

简单来讲，旋转向量就是一个向量，向量的方向表示旋转轴，向量的大小表示旋转角度，通常用符号\(\phi\)表示。为了后面便于理解，需要先引入一些概念，首先是外积： \[ \pmb{a}\times \pmb{b}=\begin{aligned}\begin{bmatrix}a_2b_3-a_3b_2\\a_3b_1-a_1b_3\\a_1b_2-a_2b_1\end{bmatrix}\end{aligned}=\begin{aligned}\begin{bmatrix}0&-a_3&a_2\\a_3&0&-a_1\\-a_2&a_1&0\end{bmatrix}\end{aligned}\pmb{b}=\pmb{a}^{\wedge}b \] 这里和普通外积一样，主要是引入一个符号\(\wedge\)，将该符号称为反对称符号，他的功能是将向量转成对应的一个反对称矩阵，还有一个符号\(\vee\)表示将对应的反对称矩阵转化为向量，这是一个一一对应的关系： \[ \pmb{a}^{\wedge}=\begin{aligned}\begin{bmatrix}0&-a_3&a_2\\a_3&0&-a_1\\-a_2&a_1&0\end{bmatrix}\end{aligned} \] 一个旋转向量可以唯一表示一个姿态，那么他对应了一个旋转矩阵，将旋转向量分解为模乘以方向的形式\(\phi=\theta\pmb{n}\)，那么旋转向量和旋转矩阵的关系由罗德里格斯公式给出： \[ R=\cos\theta I+\left(1-\cos\theta\right)\pmb{n}\pmb{n}^T+\sin\theta\pmb{n}^{\wedge} \] 同样，旋转矩阵也可以转化成旋转向量，对上述罗德里格斯公式两边同时取迹可以得到： \[ \theta = \arccos\frac{tr{(R)}-1}{2} \] 而根据旋转轴旋转后不变可得\(R\pmb{n}=\pmb{n}\)可得：旋转轴为\(R\)中特征值1对应得特征向量，根据本科求特征值特征向量得方法的知识即可求出 > 这里还是简单说一下，根据\(\left(A-\lambda E\right)x=0\)，先求\(\lambda\)再带入求解\(x\)，不过这里\(\lambda=1\)是已知结果，可以带入后直接求解对应的\(x\)

四元数

如果说欧拉角是最容易混淆的，那么四元数就是最难理解的😭。

有一些复数基础的朋友都知道复数乘以\(e^{i\theta}\)就是将复数在复平面旋转\(\theta\)（我本科做图片旋转的作业时，就是将每个点转化成复数，再乘以\(e^{i\theta}\)得到旋转后的像素坐标）。而四元数就相当于三维空间上的复数，我们先介绍以下四元数的基本概念和性质，再使用他来表示姿态。

四元数基本概念和性质

四元数一般用符号\(q\)（quaternion）表示，拥有一个实部和三个虚部，如下所示（实部不一定在前面）： \[ \pmb{q}=q_0+q_1i+q_2j+q3k \] 其中，\(i,j,k\)为虚部，他们之间满足： \[ \left\{\begin{align*}\begin{array}{l}i^2=j^2=k^2=-1\\ij=k,ji=-k\\jk=i,kj=-i\\ki=j,ik=-j\end{array}\end{align*}\right. \] 通常情况下，我们喜欢用一个标量和一个向量来表示四元数： \[ \pmb{q}=\left[s,\pmb{v}\right]^T,\ s=q_0\in R,\ \pmb{v}=\left[q_1,q_2,q_3\right]^T\in R^3 \] 如果一个四元数实部为0，称为虚四元数，若虚部为0，则称为实四元数，接下来讲解一下四元数的运算，设有两个四元数： \[ \pmb{q}_a=\left[s_a,\pmb{v}_a\right]=s_a+x_ai+y_aj+z_ak \\ \pmb{q}_b=\left[s_a,\pmb{v}_a\right]=s_a+x_ai+y_aj+z_ak \]

四元数加减法

\[ \pmb{q}_a\pm\pmb{q}_b=\left[s_a\pm s_b,\pmb{v}_a\pm\pmb{v}_b\right] \]
乘法

\[ \begin{align*} \pmb{q}_a\pmb{q}_b=& s_as_b-x_ax_b-y_ay_b-z_az_b\\ &+\left(s_ax_b+x_as_b+y_az_b-z_ay_b\right)i\\ &+\left(s_ay_b-x_az_b+y_as_b+z_ax_b\right)j\\ &+\left(s_az_b+x_ay_b-y_ax_b+z_as_b\right)k \end{align*} \] 这里其实就是两数相乘的结果，写法上，上式是保证左边字母顺序是\(s_a,x_a,y_a,z_a\)，右边就是乘积为对应维度的值，写成向量的形式有 \[ \pmb{q}_a\pmb{q}_b=\left[s_as_b-v_a^Tv_b,s_av_b+s_bv_a+v_a\times v_b\right]^T \] 根据上面所示，显然实四元数相乘仍未实四元数、虚四元数相乘认为虚四元数，且四元数的乘法不满足交换律
模长

\[ \left\|\pmb{q}_a\right\|=\sqrt{s_a^2+x_a^2+y_a^2+z_a^2} \] 两个四元数乘积的模等于模的乘积： \[ \left\|\pmb{q}_a\pmb{q}_b\right\|=\left\|\pmb{q}_a\right\|\left\|\pmb{q}_b\right\| \]
共轭

和复数一样，共轭就是虚部取相反数： \[ \pmb{q}_a^*=s_a-x_ai-y_aj-z_ak=\left[s_a,-\pmb{v}_a\right]^T \] 和复数一样，四元数和自身共轭的乘积为模长的平方： \[ \pmb{q}_a^*\pmb{q}_a=\pmb{q}_a\pmb{q}_a^*=\left[s_a^2+\pmb{v}_a\pmb{v}_a^T, 0\right] \]
逆

其实就是\(1/\pmb{q}\)，和复数类似，可以上下同时乘以共轭得到： \[ \pmb{q}^{-1}=\frac{\pmb{q}^*}{\left\|q\right\|^2} \] 显然，其逆和自身乘积为1： \[ \pmb{q}^{-1}\pmb{q}=\pmb{q}\pmb{q}^{-1}=1 \] 如果\(q\)为单位四元数，其逆等于共轭，四元数乘积的逆具有和矩阵类似的性质： \[ \left(\pmb{q}_a\pmb{q}_b\right)^{-1}=\pmb{q}_b^{-1}\pmb{q}_a^{-1} \]
数乘

\[ k\pmb{q}=\left[ks,k\pmb{v}\right] \]

四元数表示旋转

这里我主要讲解一些公式，没有几何上的解释

使用四元数表示的旋转

首先，我们需要记住一点，一个单位四元数对应了一个唯一的旋转，如果将该旋转作用在\(\pmb{p}\)点上，让其变成\(\pmb{p}'\)需要两步：

首先用虚四元数表示空间中的\(\pmb{p}=[x,y,z]\)点

\[ \pmb{p}=[0,x,y,z]^T=[0,\pmb{v}]^T \]
旋转后的点为

\[ \pmb{p}'=\pmb{q}\pmb{p}\pmb{q}^{-1} \] 这里旋转后的为纯虚四元数，其虚部为旋转后的点的坐标

和其他旋转的关系

为了和旋转矩阵扯上关系，我们先定义两个符号，用于将四元数转化成矩阵，设\(\pmb{q}=[s,\pmb{v}]^T\)，定义符号\(^+\)和\(^{\bigoplus}\)为： \[ \pmb{q}^+=\begin{aligned}\begin{bmatrix}s&-\pmb{v}^T\\\pmb{v}&s\pmb{I}+\pmb{v}^{\wedge}\end{bmatrix}\end{aligned},\ \pmb{q}^{\bigoplus}=\begin{aligned}\begin{bmatrix}s&-\pmb{v}^T\\\pmb{v}&s\pmb{I}-\pmb{v}^{\wedge}\end{bmatrix}\end{aligned} \] 有了上述符号，我们可以把四元数乘法写成矩阵的形式： \[ \pmb{q}_1^+\pmb{q}_2=\begin{aligned}\begin{bmatrix}s_1&-\pmb{v}_1^T\\\pmb{v}_1&s_1\pmb{I}+\pmb{v}_1^{\wedge}\end{bmatrix}\end{aligned}\begin{aligned}\begin{bmatrix}s_2\\v_2\end{bmatrix}\end{aligned}=\begin{aligned}\begin{bmatrix}-\pmb{v}_1^T\pmb{v}_2+s_1s_2\\s_1\pmb{v}_2+s_2\pmb{v}_1+\pmb{v}_1^{\wedge}\pmb{v}_2\end{bmatrix}\end{aligned}=\pmb{q}_1\pmb{q}_2=\pmb{q}_2^{\bigoplus}\pmb{q}_1 \] 我们就可以写出四元数和旋转矩阵的关系（证明见最后）： \[ \pmb{R}=\pmb{v}\pmb{v}^T+s^2\pmb{I}+2s\pmb{v}^{\wedge}+\left(\pmb{v}^{\wedge}\right)^2 \tag{1} \] 有了R，就可以很容易得到和旋转向量之间的关系（证明见最后）： \[ \left\{\begin{align*}\begin{array}{l} \theta = 2\arccos q_0\\ \left[n_x,n_y,n_z\right]^T=\left[q_1,q_2,q_3\right]^T/\sin\frac{\theta}{2} \end{array}\end{align*}\right.\tag{2} \]

其他变换

除了上述欧式变换之外，常见的还有如下3种变换

相似变换

相比欧式变换多了一个自由度，可以对物体进行均匀缩放 \[ \begin{aligned}\begin{bmatrix}s\pmb{R}&\pmb{t}\\\pmb{0}^T&1\end{bmatrix}\end{aligned} \]

仿射变换（正交投影）

形式如下所示： \[ \begin{aligned}\begin{bmatrix}\pmb{A}&\pmb{t}\\\pmb{0}^T&1\end{bmatrix}\end{aligned} \] 仿射变换只要求矩阵\(\pmb{A}\)为可逆矩阵，而不必须是正交矩阵，放射变换后立方体不一定是方的，单各个面仍然平行

射影变换

形式如下所示： \[ \begin{aligned}\begin{bmatrix}\pmb{A}&\pmb{t}\\\pmb{a}^T&v\end{bmatrix}\end{aligned} \] 左上角为可逆矩阵\(\pmb{A}\)，右上角为平移\(\pmb{t}\)，左下角为缩放\(\pmb{a}\)，右下角的\(v\)其实只有1和0两种取值（其他值时可以对矩阵除以\(v\)转化成1），这里左下角的意义涉及到齐次坐标的来源，可以自行百度，这里给一个介绍的还不错的博客：什么是齐次坐标? - 知乎 (zhihu.com)。

从真实世界到相机照片可以看作一个射影变换，变换后平行关系由于近大远小可能变成相交关系。

总结

各种变换之间的性质比较如下所示

变换名称	矩阵形式	自由度	不变性质
欧式变换	\(\begin{aligned}\begin{bmatrix}\pmb{R}&\pmb{t}\\\pmb{0}^T&1\end{bmatrix}\end{aligned}\)	6	长度、夹角、体积
相似变换	\(\begin{aligned}\begin{bmatrix}s\pmb{R}&\pmb{t}\\\pmb{0}^T&1\end{bmatrix}\end{aligned}\)	7	体积比
仿射变换	\(\begin{aligned}\begin{bmatrix}\pmb{A}&\pmb{t}\\\pmb{0}^T&1\end{bmatrix}\end{aligned}\)	12	平行性、体积比
射影变换	\(\begin{aligned}\begin{bmatrix}\pmb{A}&\pmb{t}\\\pmb{a}^T&v\end{bmatrix}\end{aligned}\)	15	接触平面的相交和相切